
Table of Contents
- What are embedding vectors
- Intuition
- From a piece of text to embedding vectors
- OpenAI Embeddings API
- Other Resources
What are embedding vectors
Embedding vectors are an esential element in every Natural Language Processing (NLP) system. We can’t input text into a machine learning model so we use numbers, which can be processed by it.
An embedding or embedding vector is a projection in a vector space of a piece of text (word, sentence, paragraph or a whole document), it is a numerical representation of text, a list of numbers that represent the piece of text and that holds semantic information from it.
To get the vector that represent the piece of text we need to encode the text, resulting in the embedding vector. Through this proccess, the codification of the word or sentence embeds its meaning into the vector. The embedding vector is able to capture meaning or semantics from the text used as input to create it. It holds information about how that word or sentence is used in the human language. So thanks to embeddings we have a way to make computers understand human language by encoding the text into a vector that contains meaning of that text, which can be processed by the computer as it is a list of numbers.
Intuition
Imagine that we want to represent the concepts of “puppy”, “dog”, “fawn”, and “deer” on a two-dimensional graph. If we want to draw concepts on a two-dimensional graph we need to represent those concepts as two-dimensional vectors, one for each axis of the graph. For our example, the x-axis (abscissa) is “age” and the y-axis (ordinate) is “weight” so each vector’s first dimension represent “age” and its second dimension represent “weight”.
Now that we have a two-dimensional graph and some two-dimensional vectors we can plot those vectors as points on the graph, as show below. For the sake of simplicity, let us forget the concrete values of those vectors or points.

Some facts stand out when looking at our scatter plot, we can see certain relationships between the concepts represented. The dog is more to the right on the x-axis than the puppy because it is older, and it is also higher up on the y-axis because it is heavier. The same logic would apply to the fawn and deer concepts. The deer would be more to the right on the x-axis and higher up on the y-axis because it is older and heavier than the fawn.
So we find that puppy and dog are related to each orther when considering them as a set of age and weight, as well as fawn and deer. Puppy is a dog the same that fawn is a deer. Or dog is a puppy the same that deer is a fawn.
Let’s consider the popular example of the relationships between “king”, “queen”, “man” and “woman”. In this case we can think of those concepts as two-dimensional vectors represented by points in a two dimensional scatter plot, where the y-axis would be something like the amount of royalty and the x-axis would represent the gender.

We intuitively understand the relationships between those concepts. We can think that “king” is a “man” the same that “queen” is a “woman”. But even more interesting, we can use these relationships and the vectors that represent these concepts to do some vector computations.
So we have the concepts of “king” and “queen”, both are high in royalty as they are its maximum expression. However, they differ in gender. We could extract that gender from both concepts so we would end up with something similar, as show below.
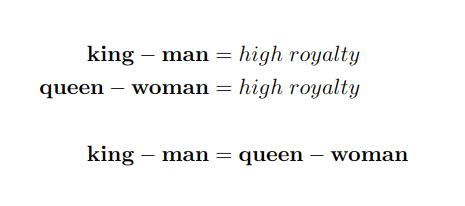
Now we can show all kind of relationships using the equation above. As in the visualization above, we could move “woman” to the left side of the equation to compute “queen”. Or we could compute “king” in a similar way. A little less intuitive is the computation of “woman” or “man”. If we rearrange the equation we have that “woman” equals to “queen” minus “king” plus “man”. The “+ man” section when computing “woman” is explained because when we extract “king”, “man” is being extracted too.

We already know how text can be represented as points in a vector space of two dimensions. But the concepts showed above are much more complex, we are not representing a lot of features from them. For instance, deer and dog have two ears and are four-legged, one could have a different skin thickness, etc. But even more, when we compute the vectors representing those words with the methods they are computed in NLP, the vectors can contain a lot of information about them, not only features that we can intuitively imagine quickly, but also the way in which they are used in our language. Extrange and abstract patterns and features are impregnated into these vectors, which contain the meaning of words or entire sentences, as complex and rich as our language allows them to be. So by computing embeddings we get feature vector representations of text sequences that are able to capture properties or features of the word. They are representations of data as points in space and that location in the space can capture some information about the meaning of a piece of text.
The resulting vectors computed with NLP techniques are much longer than two dimensions, usually from hundreds to a few thousands, and that high dimensionality allows them to hold more accurate information about the subyacent text. These embedding vectors can represent not only words, but also sentences or longer pieces of text, which can be visualized too, as we will see in the next sections of this article. We will reduce the length of those long embedding vectors with dimensionality reduction techniques (like PCA) in order to visualize them in three and two dimensional vector spaces, and we will also reduce their dimensions to ten in order to draw a beatiful image like the one at the beginning of the article.
So the takeaways in this section are the following:
- Text or human language can be represented as vectors or points in a vector space.
- Embedding vectors hold information about the piece of text the are computed from.
- Once we have the text represented as vectors we can do some computantions with them.
From a piece of text to embedding vectors
Let’s delve into the process of transforming text to vectors. This process allows us to transform words or sentences into tokens which are then converted into dense vectors.
Sparse vectors vs Dense vectors
We can consider that there are two types of vectors depending on whether they are very long and have many zeros or not. Let’s consider the sentence “pizza with pineapple is the best pizza” to see an example of sparse vectors and dense ones.
Imagine that we have a vocabulary of 30,000 words. We only know 30,000 words and every sentence we make can only be made up of those words. If we order our vocabulary in such a way that each word from the first to the last always has the same position, we can make a vector for each word with the length of our vocabulary, where every number is zero except where the word is positioned in our ordered vocabulary. For example, if “pizza” was the first word of our vocabulary its corresponding vector would be “1” in its first dimension and 29,999 zeros after it. If “with” was the second word in the vocabulary its second dimension would be “1” and the other ones zero. So for every word in the vocabulary we have a vector of 30,000 components and all but one are zeros! Those binary vectors are sparse vectors and can be obtained by one-hot encoding categorical features or by algorithms like BM25. The problem with them is that they don’t give us too much information of the text they come from.

Fortunately, we have other methods to obtain much more semantically rich vectors. They are dense vectors and they are generated from machine learning models like GloVe and Transformers. You can see each word from the sentence “pizza with pineapple is the best pizza” computed with a transformer model below. The resulting dense vectors are the 1536-dimensional embedding vector of each word. As you can see they are almost always values other than zero, which allows vectors to encode richer and more diverse patterns.

Word Embeddings and Sentence Embeddings
The two main techniques to obtain dense embedding vectors are word embedding and sentence embedding. Both use machine learning models, but sentence embeddings use transformer networks, which are much more powerful. As you can imagine, the trend today is to use sentence embeddings as they are better.
Word Embeddings
A word embedding is a way of representing an individual word as a dense high-dimensional vector, it implements language modeling and feature extraction based techniques to map words to vectors. One of the most popular techniques to create word embedding vectors is Word2Vec, created by researchers at Google in 2013. Word2Vec is a deep learning model to compute dense vector representations of words by unsupervised learning. Those learned vectors encode many linguistic regularities and patterns from text. Although there are other algorithms that can be used to generate word embeddings (GloVe, FastText, etc.) we will only explain Word2Vec briefly.
Word2Vec model
Word2Vec is a deep learning unsupervised model that takes a textual corpora and learns an embedding vector for each word. Corpora are largue and massive collections of linguistic data, which are used to train the Word2Vec models in order to learn the word vectors.
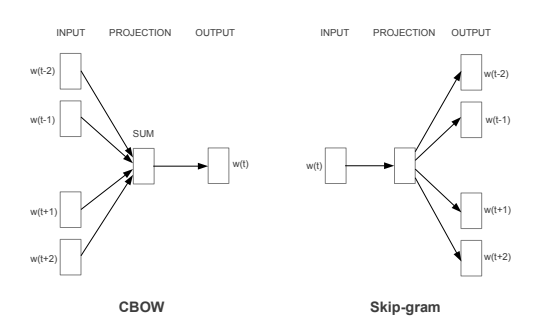
Word2Vec groups two different neural network architectures that help the network learn or create the embedding vectors. Each of them can be used to generate the word embeddings. Both are neural networks with an input layer, a single hidden layer, and an output layer. We have to train it to perform a task. Once it is trained we won’t use the network to predict something, instead we use the hidden layer weights as our embedding vectors.
The Continuous Bag of Words Model
In the CBOW model the objective is to learn word vector representations that are good at predicting the current target word based on the source context words. It tries to predict the center word (target word) based on the the context (the surrounding ones which are the model input).
The training process starts when some context words are input to the model. The context words are the words before and after the target word, the surrounding ones. If we set the context window size to 2, then the surrounding context which is input to the model consist of the two words before the target word and the two words after it. Those words are input to the input layer, which outputs a one-hot-vector of size vocab_size with value of “1” at the elements corresponding to the context words. The resulting one-hot-vector is input to the hidden layer (embedding layer) of size vocab_size x embed_size. It has as many rows as words exist in the vocabulary and as many columns as features we want the embedding vectors to have. If the hidden layer inputs a one-hot-vector representing four words, four vectors are computed and then averaged to get the averaged context embedding (of size embed_size).
Then the resulting vector from the hidden layer are input to the output layer which is a dense sofmax layer that consist of a matrix of size embed_size x vocab_size. It outputs a vector of length vocab_size, which is a probability distribution where each number represent the probability of each corresponding word to be a context word. Finally the predicted and target words are compared and the embedding layer updated using backpropagation.
Once the training process is finished the word embedding vectors are already computed. They are the weights of the embedding layer (hidden layer). So you have one already computed word embedding for each word in the vocabulary as this layer is a matrix of vocab_size x embed_size. Notice that you are not training a model and then using it to predict something, you are training a model and when it is trained you have what you are looking for in its hidden layer. The final goal of the training is to adjust those weigths and use them as word embedding vectors.
The Skip-gram Model
In the Skip-gram model the training objective is to learn word vector representations that are good at predicting the nearby words. It tries to predict the context (surrounding words which are the targets) based on the center one (which is the model input).
This architecture is very similar to CBOW. However, the training samples are pair of words, the center one and one word from its context (for that center word we have several pair sentences until we have covered all its surrounding words). The center word is the model input and the context word is the target. If we set the window size to 2, we will have four training samples: (word_input, word_target_1), (word_input, word_target_2), (word_input, word_target_3), (word_input, word_target_4). Word target 1 and 2 are the two words before the center one, and the word target 3 and 4 are the words after it.
The center word (input word) is input to the model and converted to a one-hot-vector of length vocab_size in the input layer. The resulting one-hot-vector is input to the hidden layer of size vocab_size x embed_size, like in CBOW architecture. As the one-hot-vector has only an element with value equals to “1” at the position corresponding to the input word, the hidden layer outputs a vector of size embed_size that comes from the row corresponding to that input word.
Then the resulting vector from the hidden layer are input to the output layer which is a dense sofmax layer that consist of a matrix of size embed_size x vocab_size, like CBOW architecture. It also outputs a vector of length vocab_size, which is a probability distribution where each number represent the probability of each corresponding word to be a context word. And finally the predicted and target words are compared and the embedding layer updated using backpropagation.
Again, the embedding vectors we are looking for are hidden layer weights.
If you want to go deeper into these algorithms you can read the original papers “Distributed Representations of Words and Phrases and their Compositionality” by Mikolov et al. and ”Efficient Estimation of Word Representations in Vector Space” by Mikolov et al. and some very helpful resources like “Implementing Deep Learning Methods and Feature Engineering for Text Data: The Continuous Bag of Words (CBOW)” from Dipanjan Sarkar or Chris McCormick’s blog Word2Vec Tutorial - The Skip-Gram Model.
A couple of important nuances that should not be overlooked and that differentiate these vectors from those computed via sentence embeddings is that at the end of the process we already have computed embedding vectors and they are always the same, they does not change. We have a vector for each word computed with this architecture and the data provided to train the network and if we want new vectors we have to change the network or the data and train it again. The other important point is that we do not consider the order of the words, since when calculating the average of the context word embeddings to get the final embedding vector which is used to predict the target word in CBOW the order is not consider. The order is also not considered when training the Skip-Gram model as its inputs are word pairs.
Sentence Embeddings
Sentence embeddings are much more powerful than word embedidngs because they are vector representations of text sequences (instead of individual words) and can capture its meaning and context. While word embeddings just examine one word at a time, sentence embeddings can see the whole sentence or document and can understand the words order as well. Even more magical, sentence embedding can work for sentences that contain words not seen in the training set (word embeddings only make vector representations of the vocabulary).
The dominate approach to computing embedding vectors was computing embeddings of the words individually and then take the average of the corresponding dimensions. So if you had a sentence made of three words and you compute an embedding vector for each one, then you would take the first dimension of each one and take the average, resulting in the first dimension of the sentence embedding. But not anymore.
The State-Of-The-Art for computing sentence embedding vectors consists on using a pre-trained transformer neural network to compute a context-aware embedding vector of each word in the sentence and then take the average of those vectors to get the embedding of that sentence. When computing the embedding vector of each word the transformer model is able to see the entire sentence, so the final representation of that word is an embedding which contains information about the word’s position relative to the other words in the sentence. This is a really important point to highlight. By using transformer neural networks to generate embedding vectors we are leveraging positional encoding, self-attention, and multi-head attention thatks to its architecture.
With transformer neural networks we can get embedding vectors of sentences that are computed from embedding vectors of words that contains information about the word and its relation with the other words in the sentence thanks to the attention mechanism. The same word can mean different things in different sentences or positions, and the transformer network is able to capture all that meaning and represent it through a embedding vector representation. By doing this we can generate much more powerful and sophisticated embeddings which can understand word ordering.
Training of embedding models
These embedding models that we use to compute embedding vectors need to be trained in order to be able of making accurate predictions of embedding vectors. Their internal parameters need to be adjusted by training on a large corpora, and only then will the model have learnt the complex patterns of our language.
So the first step is to train the transformer neural network on a lot of unlabeled text data. After this we have a language model that can process text, it produces word vectors that captures meaning. Then we can fine-tune the model to solve a language problem like translation or question answering. The problem arise when we want to compute the similarity between sentences. We could fine-tune the network to predict the similarity between two sentences, and that would work. But the problem with this approach is that if we have a dataset of hundreds of thousand of sentences, every single time that we had a new sentence and we wanted to compute the similarity between this sentence and those in our dataset, we would have to run the forward pass one time for every sentence in our dataset. This could end up being really expensive.
The solution to this problem is to fine-tune the model to predict a single vector given a sentence as input. Now we only need to compute an embedding vector for each sentence in our dataset and save them. When we want to compute the similarity between a new sentence and all the sentences in our dataset we only need to predict the embedding vector of the new sentence and then compare it with the others using cosine similarity, which is much cheaper.
The technique used in the fine-tuning process is called contrastive learning. The model is trained to predict similar embedding vectors for similar sentence pairs and dissimilar embedding vectors for dissimilar sentence pairs, achieving a model capable of generating better sentence embedding vectors, resulting in better metrics on semantic similarity tasks.
This process and why we need so many steps to train the embedding model to obtain meaningful sentence embedding vectors is very clearly explained by Ajay Halthor here. I highly recommend it if you want to have a deeper understanding of the process.
OpenAI Embeddings API
We already now that embedding vectors are the way in which we represent the text as vectors of floating point numbers and we also have a basic understanding of how the models that we use to learn them are trained. Now let’s compute some of them to build a two cool visualizations. To compute the embeddings we will use the text-embedding-ada-002 embedding model from OpenAI, which output embedding vectors of 1536 dimensions.
You can find the code to compute the embeddings and build visualizations in this repo.

Scater plots
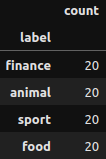
To build the visualizations below we have 80 sentences:
- 20 sentences about food
- 20 sentences about animals
- 20 sentences about finance
- 20 sentences about sports
The aim here is to visualizate them in a vector space. To achieve this we follow these steps:
- Get OpenAI API key
- Load and prepare data
- Compute embedding vectors
- Reduce data dimensionality
- Visualizations
Get OpenAI key
The OpenAI API uses API keys for authentication. I have my secret key saved in the .env file. There is a .env.example file in the repository as example. We use the function load_dotenv to read the .env file and adds the key, value pair to environment variable. Then we only need to get it with the help of the os library.
import openai
import os
from dotenv import load_dotenv
# Read .env and add key, value pairs to environment variable
load_dotenv()
openai.api_key = os.getenv('OPENAI_API_KEY')
Load and prepare data
Now we need to load and concatenate the four csv files with the sentences. Each type of sentences (finance, food, animal, and sport) is already labeled.
def concat_data(dir_path: str='./data') -> pd.DataFrame:
"""Load CSV files from dir_path and concatenate them into a df.
Args:
dir_path (str): Path to data.
Returns
pd.Dataframe: Concatenated DataFrame.
"""
df = pd.DataFrame()
for file_path in os.listdir(dir_path):
path = os.path.join(dir_path, file_path)
if os.path.isfile(path) and 'csv' in file_path:
topic_df = pd.read_csv(path, sep=',')
df = pd.concat([df, topic_df], ignore_index=True)
return df
data_80_path = './concatenated_data/data_80.csv'
concat_data().to_csv(data_80_path, index=None)
pd.DataFrame(data_80.label.value_counts())
Compute embedding vectors
We will use the get_embedding function provided for OpenAI to get the embeddings. We need to set the model we want to use in the parameteres.
from openai.embeddings_utils import get_embedding
# embedding model parameters
embedding_model = "text-embedding-ada-002"
embedding_encoding = "cl100k_base" # encoding for text-embedding-ada-002
max_tokens = 8000 # maximum for text-embedding-ada-002 is 8191
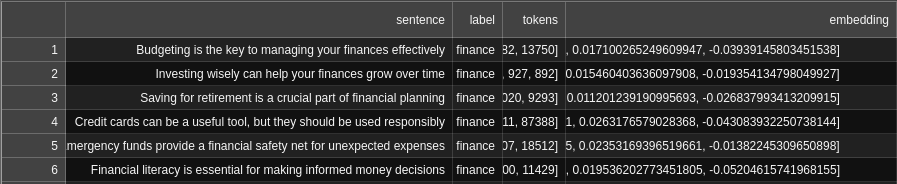
data_80["embedding"] = data_80.sentence.apply(lambda x: get_embedding(x, engine=embedding_model))
Now we should have a DataFrame containing a new column for the embedding vectors:
Once we have the embedding vector for every sentence we can reduce their dimensionality and visualizate them. Let’s do it! 💃🏽
Reduce data dimensionality
But first we need to do a little modification. The embeddings are saved as strings in the DataFrame and we need them to be lists. In order to chieve this we can use the Python ast module (Abstract Syntax Tree), which allows us to interact with and modify Python code. The ast.literal_eval function can be used for evaluating strings containing Python values without the need to parse the values oneself. By applying this funtion to every embedding we convert it from a str to a list.
# The ast.literal_eval() method is a function that evaluates a string as a literal expression, and returns the result
print('Type embedding data point:', type(df.loc[0, 'embedding']))
df['embedding'] = df.embedding.apply(lambda x: ast.literal_eval(x))
print('Type embedding data point:', type(df.loc[0, 'embedding']))

Then we convert the embedding Series to an array of shape (80, 1536) since we have 80 vectors of 1536 dimensions each.
embeddings = np.array(df.embedding.tolist())
print('Shape:', embeddings.shape)

Now we are ready to reduce the data dimensionality. For this we will use PCA (Principal Component Analysis), which is a statistical technique for reducing the dimensionality of a dataset. It summarizes a dataset containing a high number of dimensions or features per observation, increasing the interpretability of data while preserving the maximum amount of information, and enabling the visualization of multidimensional data.
1536 dimensions -> 2 dimensions
from sklearn.decomposition import PCA
two_dim_embeddings = PCA(random_state=0, n_components=2).fit_transform(embeddings) #[:,:3]
print('Shape:', two_dim_embeddings.shape)
two_dim_embeddings[:5]
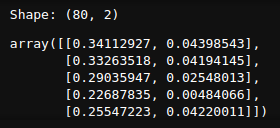
1536 dimensions -> 3 dimensions
three_dim_embeddings = PCA(random_state=0, n_components=3).fit_transform(embeddings) #[:,:3]
print('Shape:', two_dim_embeddings.shape)
three_dim_embeddings[:5]
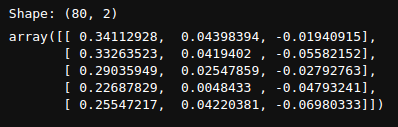
By applying PCA we are losing a lot of information from our embeddings but it will keep enough to allow us to observe different patterns in the data.
Visualizations
So let’s visually explore our new reduced vectors. As you can see in the image below, when we plot our two-dimensional vectors we can see that they have been clustered into four well-differentiated groups. The sentences related to food are close to each other, and the same is true for the other types of sentences. However we can see a small overlap between animal and sport sentences. It may be entirely possible that that two types of sentences are slightly overlapped, however in this case this is due to the loss of information that occurs in the dimensionality reduction process with PCA.
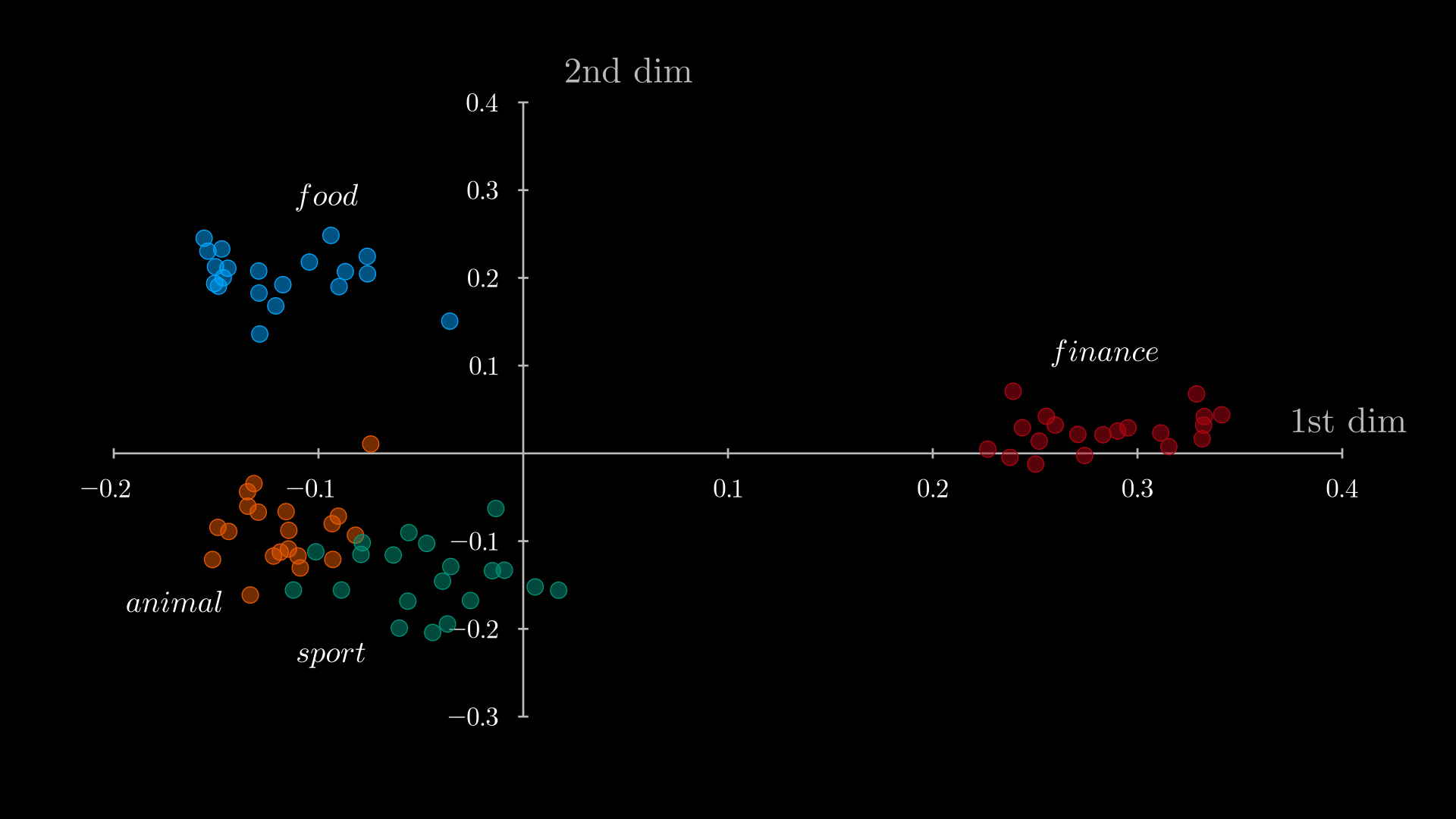
We can easily see this phenomenon if we represent the same sentences in a three-dimensional vector space. In this way we can see that the different clusters are clearly separated from each other.

This visualizactions have been made with Manim, a powerful mathematical animation engine. You can find the scripts to generate them in the repo.
High dimensional visualization
I find really interesting visualizing embeddings with a few more dimensions. To achieve this heat maps are very convenient. It allows us to visualize the value of the features and to observe various patterns.
Let’s reduce the embeddings dimensionality to ten and then plot their dimension values with a heat map.
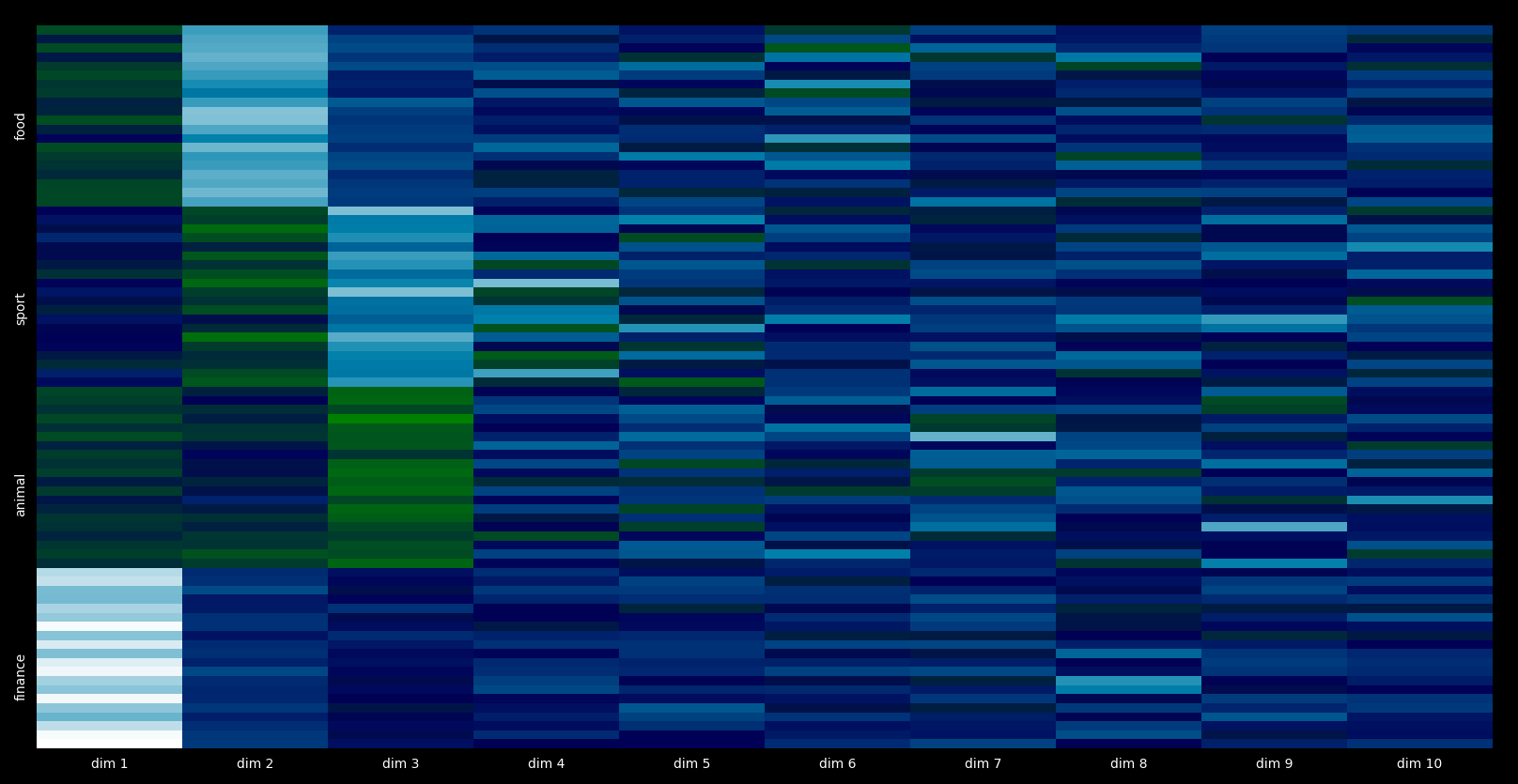
So we can see eighty sentences ordered along the y-axis. The first twenty ones are related to finance and the color of the first dimension of them is close to white, which indicates that their value is similar. In the same way, similar patterns can be observed in related sentences, which is quite beautiful.
Finally, there are a lot of possible applications for these embeddings, some of the most common ones are:
- Search (where results are ranked by relevance to a query string)
- Clustering (where text strings are grouped by similarity)
- Recommendations (where items with related text strings are recommended)
- Anomaly detection (where outliers with little relatedness are identified)
- Diversity measurement (where similarity distributions are analyzed)
- Classification (where text strings are classified by their most similar label)
Below I leave some resources that helped me to understand this topic better.
Feel free to contact me by any social network. Any feedback is appreciated!
Thanks for reading 🙂
Other Resources
- The Embedding Layer by Kunter Phillips
- Contrastive Learning for Natural Language Processing by ryanzhumich
- Full Guide to Contrastive Learning
- Sentence Transformers - EXPLAINED!
- Top 4 Sentence Embedding Techniques using Python
- Word2Vec Tutorial - The Skip-Gram Model
- Word2Vec Tutorial Part 2 - Negative Sampling
- Distributed Representations of Words and Phrases and their Compositionality
- Efficient Estimation of Word Representations in Vector Space
- Implementing Deep Learning Methods and Feature Engineering for Text Data: The Continuous Bag of Words (CBOW)
- King - Man + Woman = Queen: The Marvelous Mathematics of Computational Linguistics
- Understanding Word Embedding Arithmetic: Why there’s no single answer to “King - Man + Woman = ?”
- From Word Embeddings to Sentence Embeddings — Part 1/3
- From Word Embeddings to Sentence Embeddings — Part 2/3
- From Word Embeddings to Sentence Embeddings — Part 3/3